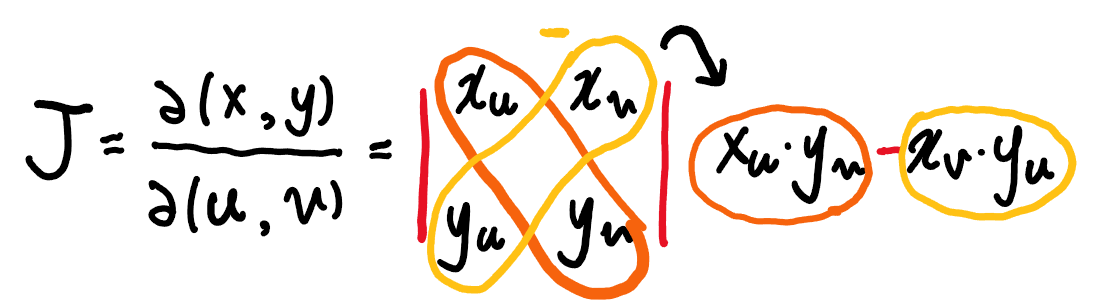datavwy 님의 블로그

이제 변수변환에 대하여 공부하였다.  변수변환을 이용해서  확률변수의 합과 차로 된 새로운 확률변수의 분포를 구해보기로 한다.  x1과 x2로 구성된 새로운 확률변수를 Y라고 하자. 그리고 X1를 x1으로 고정시키자.  Y를 결정하는 x1,x2 에 대한 식 을 u(X1, X2) 라고 할때, X1은 x1로 고정되어 있으므로 Y = u(X1, X2) 은 일변수함수처럼 생각할 수 있다.  추가적으로,  X2 가 단조함수라면, Y와 X2의 관계는 1:1 대응 관계이고 , 따라서 변수변환이 가능해진다.   즉 앞서 익숙하게 접하던 일변수 함수의 X2에서 Y로의 변수 변환 문제로 접근할 수 있다.  따라서  Y의 확률밀도 함수 fy(y)는 다음과 같다.    f( x1, x2)*J를 한 후 여기서 fy(y)를 구하..

변수변환과 관련된 예제문제를 풀어보자  예제1     X가 균등분포를 따른다고 한다. 이때 균등분포를 f(x) 라고하자. 균등분포는 정의에 의해서 [0, 1] 범위에서 f(x) = 1 이다. ( 확률의 합은 1이므로 , 가로* 세로 = 1 이어야 함 따라서 f(x) = 1)  Y = - 2InX 로 표현되었다. 즉 Y는 x에 관한식 ( = u(x) 이라하자)으로 표현할수 있고  u(x)의 역함수를 w(x) 라고 표현하면, w(x)는 e^(-y/2)  이다.  Y의 분포를 구하는 것이 문제이므로 , g(y)를 Y의 분포라고 하자.  일변수의 변환에서 g(y)의 식은  g(y) =ㅊ 이다.  w(y) 과  J 를 구하면 된다.  J는 일변수 변환의 경우 w'(y) 이므로    구한 J와 w(y)를 g(y)=..

이전 강에선 이산형 확률변수 - 1변수 , 2변수 의 변수변환을 어떻게 하는가에 대해서 배웠고  이어서 연속형 확률변수 - 1 변수 , 2변수의 변수변환을 어떻게 하는가에 대해서 배워보자.  학습하기전에 연속형 확률변수의 확률은 함수값 자체가 아닌, 함수를 적분한 값이다.  연속형 확률변수의 1변수변환의 경우 , 적분 식의 변수를 다른 변수로 변환하는 치환적분을 생각하고 ,  2변수변환의 경우 , 적분 식의 변수를 다른 변수로 변환하는 치환적분을 생각하되,  2변수를 또다른 2변수로 치환해야하므로 이중적분의 변수변환을 생각해야한다.  그리고 이중적분을 변수변환할 때 야코비안을 사용한다.  야코비안은 28장에서 베타분포를 공부할 때 언급된 적이 있는데  32강에서도 여러번 나오니깐 다시한번 복습해보자   ..

22강 부터 31강 까지 연속형 확률분포의 대표적인 유형을 배웠다.  일반적인 정규분포에서 시작해서 감마분포, 지수분포 , 카이제곱분포, 로그정규분포.. 와이블분포... 이변량정규분포와 마지막에 다변량정규분포까지 다채롭게 배웠다 이번에는 다른 주제로  확률분포의 확률변수를 변환하는 방법에 대해서 7장으로 넘어가 배워보기로 한다.   6장에서도 살짝 배웠지만 조금 본격적으로 배우는 느낌인 것같다.  크게 이렇게 배울것 같다.   1. 이산확률변수의 일변수 함수의 확률변환 2. 연속확률변수의 일변수 함수의 확률변환 3. 이산확률변수의 이변수 함수의 확률변환 4. 연속확률변수의 이변수 함수의 확률변환   여기서 제일 어려울 건 4번인 것 같다.     X는 확률분포 f(x) 인 이산형 확률변수 ,  확률변수 ..

하나의 전형에는 여러가지 시험이 있을 때,  1차 필기시험점수 , 2차 필기시험점수  , 면접 점수 .. 각각의 점수마다 정규분포를 이룬다고 할 때, 다변량 정규분포를 생각할 수 있다.   여러개의 확률변수를 하나의 열 벡터로 생각하려고 한다.  각 벡터의 원소들(요소 또는 성분 그냥 각각 확률변수를 말함 )  사이에 연관성이 존재하는데  연관성은 공분산으로 생각하기로 한다.  벡터와 행렬의 개념을 통해  (1) 확률변수들의 묶음  (2) 평균들의 묶음  (3) 공분산들의 묶음  을 정의해보기로 한다.  정의하고 나면, 다변량 정규분포의 식을 정리할 수 있다.    (1) p 개의 확률변수 X1 , X2 , ... , Xp 에 대해서  이 확률변수들을 세로로 늘여뜨려놓은 열벡터를 다변량 확률변수(또는 확..

29장에선  X가 정규분포를 따른다고 가정하고  X = x 로 고정일때 Y의 조건부 확률분포가  정규분포를 따른다 가정한 뒤 ,  이변량 정규분포를 열심히 증명했다.    이번에는 역으로 이변량 정규분포가 주어질때  X가 정규분포를 따르고   X = x일때 Y의 조건부확률분포가 정규분포를 따른다 는 것 을 증명한다.    (1) 증명   우선 fx(x) 라는 x의 주변분포의 식을 f(x , y)를 이용해서 작성한다.      해당 식에서 x와 관련된 묶음들을 일부 꺼내오고 이를 g(x) 라고 둔다.   다음은 dy를 dw로 변환한다.  w는 y에 대한 일차식이므로, y가 -∞ ~ ∞ 까지 움직이면, w 도 -∞ ~ ∞ 까지 움직인다.    그 다음   e의 지수안에 식을 완전제곱식으로 바꾼다. 완전제곱식..

조건부 평균과 조건부 분산   -- 복습 --  X = x 가 일어날 확률은 f(x) 이라는 일변수 함수 형태의 확률밀도함수를 이용하여 값을 구했다.  그렇지만 두개의 확률변수가 주어질때 확률은  f(x, y) 이라는 이변수 함수 형태의  결합확률밀도함수를 이용하여 값을 구한다고 배웠다.  또한 주변분포함수도 배웠는데,  주변분포함수란, 결합 밀도 함수가 주어졌을 때, X만의 , 혹은 Y만의 확률을 구하고 싶을 때 쓰고싶은 확률밀도 함수 형태이다.  보통  X만의 주변분포함수를 g(x) 라고 표현하고 Y만의 주변분포함수를 h(x) 라고 표현하는데 정하기 나름이다.   X, Y 의 결합 확률밀도함수가 f(x, y) 이고, 각각의 주변분포함수를 fx(x), fy(y) 라고 하자.   X = x 로 주어질 때..

베타함수에 대해 알아야한다.  베타함수    베타함수가 적분의 형태로 되어있다는 점에서  감마함수와 유사하다. (감마함수도 적분의 형태로 함수가 주어졌으니깐)   베타함수의 성질이 이렇게 2개가 있는데 하나씩 증명해보자    B( α, β ) 자리에 α 대신 β 를 대입  β 대신 α 를 대입해서 B( β, α ) 식을 써보자  그다음 1-x = t 로 치환해주고 식을 정리하면   B( β, α ) 가  B( α, β ) 랑 같아진다.       (2)를 증명하기 위해서는  야코비안을 이용한 이중적분의 변수변환 을 하는법 을 알아야한다.    위의 그림처럼  x가 u 와 v 변수를 갖는 형태로 되어 있고,  y 역시 u와 v 변수를 갖는 형태로 되어 있을 때,  일단   J 즉 야코비안을 어떻게 표현할까..

카이제곱분포  카이는 X 를 그리스어로 표현한 말이다.  χ에 제곱을 한다고 해서 카이제곱분포라고 불린다.  사실 카이제곱분포는 감마분포의 특수한 경우이다.  한마디로 감마분포의 일종인데, 카이제곱분포가 실생활에 많이 쓰여서  따로 카이제곱분포라고 이름이 붙여졌다.  (구체적으로, 카이제곱분포는 통계적 추론에서 중요한 역할을 하는데, 정규모집단의 모분산을 통계적으로 추론할때 쓰인다. 나중에 추론할때 카이제곱분포가 나오니깐 기억해두자)   즉 카이제곱분포(chi-square distribution)는    α = ν / 2 ( ν 는 양의 정수) 이며, β = 2 인 감마분포이다.   생뚱맞게 ν가 있는데 ν는 카이제곱분포의 자유도를 나타낸다.  그래서 카이제곱분포를 자유도 ν 인 카이제곱분포라고 부른다...

25강에서는 감마분포와 지수분포와 관련된 문제를 풀어본다.   그전에 감마분포와 지수분포가 포아송 분포와 관련이 있다는 점을 알아야한다. 24강 마지막 부분에 있는 내용인데 25강에 더 어울리는 것 같아서 소개함   포아송 과정과의 관계   먼저 포아송 분포에 대해 복습을 한다면,  포아송 분포란 어떤 길이의 시간이나 공간에서 우리가 집중하는 사건이 평균   μ = λt 번 발생할 때 실제로 x 번 발생할 확률을 나타내고  기호로 p ( x; λt ) 혹은 p( x ; μ ) 라고 표시한다.  포아송 분포의 확률변수가 x 번인 것을 생각해 본다면,   포아송 분포는 포아송 과정에서 일어나는 횟수에 주목한다.  이제부터 한단계 나아가서  포아송 과정에서 조금 다른 시야로 주목해보자 횟수에 주목하기 보다 시..