이전 강에선 이산형 확률변수 - 1변수 , 2변수 의 변수변환을 어떻게 하는가에 대해서 배웠고
이어서 연속형 확률변수 - 1 변수 , 2변수의 변수변환을 어떻게 하는가에 대해서 배워보자.
학습하기전에
연속형 확률변수의 확률은 함수값 자체가 아닌, 함수를 적분한 값이다.
연속형 확률변수의 1변수변환의 경우 , 적분 식의 변수를 다른 변수로 변환하는 치환적분을 생각하고 ,
2변수변환의 경우 , 적분 식의 변수를 다른 변수로 변환하는 치환적분을 생각하되,
2변수를 또다른 2변수로 치환해야하므로 이중적분의 변수변환을 생각해야한다.
그리고 이중적분을 변수변환할 때 야코비안을 사용한다.
야코비안은 28장에서 베타분포를 공부할 때 언급된 적이 있는데
32강에서도 여러번 나오니깐 다시한번 복습해보자
< 연속형 확률변수 - 1변수 >
X라는 연속형 확률변수가 있고
X의 확률분포를 f( x )라고 할때 ,
X로 이루어진 Y의 확률분포는 어떻게 구할까? 에 초점을 맞춘다.
( = 연속형 확률변수 - 1변수를 변환하는 법 )
중요한 점은 Y와 X가 1: 1 대응 관계여야한다는 점이다.
물론 마지막에 이르러선 1: 1 대응 관계가 아니더라도 변수를 변환하는 법에 대해서 배울 것이지만
지금은 일단 Y = u ( X ) 가 1: 1 대응 관계임을 가정하고 X변수를 Y변수로 변환해보자
1:1 대응 관계를 갖는 함수는 두가지가 있다. 하나는 증가함수 , 또 다른 하나는 감소함수
따라서 먼저 y = u ( x ) 가 증가함수인 경우 부터 생각해보자
(1) y = u ( x ) 가 증가함수인 경우 ( = 접선의 기울기가 양수 )

P ( a < Y < b ) 를 구하는 것에 관심이 있다.
위의 그림을 보면, x와 y의 역함수 관계가 성립되어서
x가 결정되면 y가 결정되고 , 반대로 y가 결정되면 , x가 결정된다.
구체적으로 x가 결정되면 u( x ) 식 ( = 규칙) 에 따라서 y가 결정되고
y가 결정되면 u( x ) 의 역함수인 w ( y ) 식 ( = 규칙) 에 따라서 x가 결정되므로
Y가 a < Y < b 범위에 있을 확률은
X가 w(a) < X < w( b) 범위에 있을 확률과 같다.
P ( a < Y < b ) = P ( w( a ) < X < w ( b ) )
X의 확률은 X를 구간에 따라 적분한 값이다.
이때, X에 대한 식을 Y에 대한 식으로 바꾸기 위해서 치환적분을 사용한다.

P ( a < Y < b ) 의 식이 마지막의 적분 식이므로
적분 안의 식은 확률변수 Y의 확률밀도함수인 g ( y ) 이다.

f( w ( y ) ) * w'( y) 가 g( y ) 가 되는데
이때 w( y) 의 도함수는 야코비안이다.
일변수 함수에서 야코비안은 w ( y ) 의 도함수 이다.
w ( y ) 는 u ( x ) 의 역함수 이다.
u'( x ) 는 접선의 기울기이고 ,
역함수의 기울기는 접선의 기울기의 역수 이고 현재 접선의 기울기는 양수이므로
w'( y ) 는 양수이다.
w'( y ) = J 는 양의 값을 가지므로 ,
J값과 J에 절댓값을 씌운 값은 서로 같다.
따라서 y = u ( x ) 가 증가함수인 경우에
Y의 확률밀도함수는 다음과 같다.

이번에는 y = u ( x ) 가 감소함수인 경우 Y의 확률밀도함수 g ( y )는 어떤지 확인해보자
(2) y = u ( x ) 가 감소함수인 경우 ( = 접선의 기울기가 음수 )

P ( a < Y < b ) 를 구하는 것에 관심이 있다.
위의 그림을 보면, x와 y의 역함수 관계가 성립되어서
x가 결정되면 y가 결정되고 , 반대로 y가 결정되면 , x가 결정된다.
구체적으로 x가 결정되면 u( x ) 식 ( = 규칙) 에 따라서 y가 결정되고
y가 결정되면 u( x ) 의 역함수인 w ( y ) 식 ( = 규칙) 에 따라서 x가 결정되므로
Y가 a < Y < b 범위에 있을 확률은
마찬가지로 X가 w(b) < X < w( a ) 범위에 있을 확률과 같다.
하지만 이번에는 w ( a ) < Y < w( b ) 범위가 아닌 w(b) < X < w( a ) 범위 이다.
감소함수라서 x가 증가하면 y가 감소하기 때문에 , 범위가 (1) 의 경우와 다르게 표현이 뒤바꼈다.
P ( a < Y < b ) = P ( w( b ) < X < w ( a ) )
X의 확률은 X를 구간에 따라 적분한 값이다.
이때, X에 대한 식을 Y에 대한 식으로 바꾸기 위해서 치환적분을 사용한다.

(1) 과 다르게 적분 범위에 주목해보자!
b부터 a 까지 f( w ( y ) ) * w'( y) 를 y에 대하여 적분한다.
그래프를 보면 b가 a보다 크기 때문에,
일반적으로 작은 수 부터 큰 수 까지 적분을 하는 관념?? 상
바꿔줘야한다.
적분범위를 뒤바꿀땐 앞에 마이너스를 붙여줘야한다.
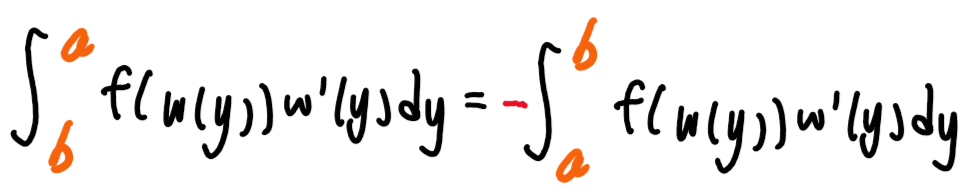
w' ( y ) 는 역함수의 기울기를 뜻하고
역함수의 기울기는 접선의 기울기의 역수이다.
(2) 에선 접선의 기울기는 음수이므로
w' ( y ) = J
J 는 음수이다.
따라서 야코비안에 절댓값을 씌운 값은 야코비안에 음수를 취한 값과 같다.

g( y ) 의 식이 ( 1 ) 에서 도출한 g ( y ) 식과 같아졌다.
(1) 과 ( 2) 를 종합해보면,
연속형 확률변수 의 1변수 변환의 경우
g ( y ) 의 식은 다음과 같다.

이번에는 연속형 확률변수 - 2변수 일 경우 변수변환을 어떻게 하는지 살펴보자
< 연속형 확률변수 - 2변수 >

연속확률변수의 2변수 변환을 다룰 때 까다로운 부분이 '범위 ' 인것 같다.
범위를 고려할 땐,
x1 범위 따로 x2 범위 따로 고려하는게 아닌,
x1 범위와 x2 범위가 이루는 평면의 구간을 생각한다.
x1 범위와 x2 범위가 이루는 평면을 R이라고 하면
해당 R을 y1 범위와 y2 범위가 이루는 평면 S로 변환하여야 한다.
예시를 통해서 변환을 어떻게 하는지 구체적으로 알아보자

우선, Y와 X 가 1: 1 대응 관계에 있는지 확인해야한다.
0 < x1 < 1 이므로 , Y1 = X1^2 는 주어진 범위에서 1: 1 대응 관계가 된다.
그다음 Y1 와 Y2의 결합확률분포를 구하기 위해서,
X1 과 X2를 y1, y2 에 대하여 각각 정리해보고 , 야코비안을 구해보자

그 다음 x1 , x2가 이루는 평면의 영역이 주어져 있고 ,
y1 = x1^2, y2 = x1*x2 로 y1과 y2가 x1, x2 에 대한 식으로 주어져 있을 때,
y1와 y2 가 이루는 평면의 영역은 어떤가?를 알아야 변수변환을 할 수 있다.
즉 x1x2 평면의 영역을 A라고 하면, 0 < x1 < 1, 0< x2 < 1이므로
A는 길이가 1인 정사각형 만큼을 영역으로 가진다.
이때 y1와 y2가 y1 = x1^2, y2 = x1*x2 이렇게 구성되어 있다면
y1와 y2가 이루는 평면의 영역을 구해야한다.

이 경우엔 경계선을 먼저 파악해야한다.
28강에서도 변환하는 경우 , 변환할 때 범위를 파악하기 위해서 먼저 경계선을 고려해주었다.
범위가 경계선의 바깥쪽의 영역을 빠져나가지 않는다고 생각하면,
범위는 경계선 안쪽의 영역에 해당하기 때문이다.
해당 예제의 경우 ,
A 영역의 정사각형 둘레가 경계선으로 하고
경계선 x1 = 0 , x2 = 0 , x1 = 1, x2 =1 을 일단 기준으로
y1과 y2로 둘러싼 영역 B는 어떤지를 생각하면 된다.
사실 추가적으로 x1 = 0 이 된다면, y1 = x1^2, y2 = x1*x2 식에 의해서
y1과 y2 모두 0 이 되기 때문에, B영역에선, x1 = 0 일 경우 , 원점으로 모이게 될 것이다.
최대한 A 영역의 경계선을 이용해서 B 영역의 경계선을 파악하는 것이 중요하다.

B 의 경계선은 y1 = 0 , y2 = 0 , y2 = 1 , y2 = 루트y1이 된다.
이를 토대로 B의 영역을 그리면,

B의 영역을 수식으로 표현하는데 두가지 방법이 있다.
수식을 표현할 때, 순서가 중요한데
이는 이중적분시, 안쪽에 대한 적분 , 바깥쪽에 대한 적분을 표기하는 것과
관련이 있다.

이 뜻은, y1의 전체적인 범위 ( 0 부터 1까지) 를 생각한 다음
범위중 한 곳을 선택하여 y1을 고정한다음, y2의 범위를 생각한다는 뜻이다.

이 뜻은 y2를 먼저 생각한 다음 y1의 범위를 이후 생각했을 때 범위를 뜻한다.
y2가 0 부터 1 까지 움직인다고 생각할때,
그 범위중 한곳에 y2를 고정시킨 후 , y1이 어떻게 움직이는 지 파악한다.
y2를 고정시킬 때, y1의 범위는 y2^2 < y1 < 1 이다.
이렇게 B의 영역을 두가지 방식으로 표현할 수 있다.
첫번째 방식을 선택한다고 하면, 이제 Y1, Y2의 결합확률분포 식을 적을 수 있다.

이번에는 X와 Y가 1대1 대응이 아닌 경우 (연속형) 에 대해서 생각해보자
1대1대응이 아니면, 변수변환이 안된다고 했는데 , 구체적으로 말하면,
1대1 대응이 안되는 구간을 쪼개서 1대1 대응이 되게끔 만들면 된다.
해당 경우 어떻게 변수 변환을 할 수 있는지 예제를 통해서 생각해보자
X와 Y가 1대1 대응이 아닌 경우 (연속형)


( 1 ) 1 < y < 4 구간 에서의 y의 확률분포 g( y ) 구하기
구간 1 < y < 4에서는 1대 1 대응 관계가 성립하므로 ,
연속형 확률변수 x를 y로 변환할 때 사용하던 식을 그대로 이용하면 된다.
( g( y ) = f ( w( y ) ) * ( J의 절댓값) , w(y ) 가 x에 대한 y의 식이라고 할때 )
(2 ) 0 < y < 1 구간에서의 y의 확률분포 g( y ) 구하기
이 경우 0 < y < 1 에서는 1: 1 대응 관계가 성립하지 않는다.
해결하는 방법은 대응되는 x 구간 - 1 < x < 1을
역함수가 존재하는 부분들의 구간들이 되도록 분할하는 것이다.

이제 여기서 각각의 확률을 구해보자
0과 1 사이의 a , b 에 대해서 P( a < Y < b ) 의 확률은
x와 y가 1대1 대응이 아니므로 , 두가지 사건이 일어날 경우의 합이 된다.

x 의 확률은 x에 대한 적분으로 바꿀 수 있다.

이제 x에 대한 적분 식을 y에 대한 적분식으로 변환을 할 건데
주황색과 노란색 각각
x가 결정되면 y가 결정된다는 점에서 동일하지만
(각각은 이제 x와 y의 관계가 1:1 대응이다 )
어떻게 y가 결정되는지 규칙이 다르다
주황색은 x = - √ y 의 규칙을 따르고
노란색은 x = + √ y의 규칙을 따르기 때문에
각각을 따로 변수변환을 해야한다.

이제 여기서 J1 과 J2 가 구체적으로 무엇인지 살펴보면

따라서

그리고 J1과 J2를 식에 대입하면,

구간 ( 1 ) 1 < y < 4 와 구간 (2) 0 < y < 1 를 종합해보면 , g ( y ) 는 다음과 같다.

다음 문제를 풀면서 Y가 X로 변환할 시, 1: 1 대응이 아닌 경우, Y의 확률분포를 구하는 방법을 다시 학습해보자

이때 새로운 확률변수 Z 를 만든다.
Z는 ( X - μ ) / σ 로 놓으면 , Y는 Z^2 이 된다.
Z를 만든 이유는 표준정규분포를 이끌어 내기 위함이다.
Z는 표준 정규분포를 따르기 때문에 , f( z ) 는 표준 정규분포 식이 된다.
Y와 Z 와의 관계를 통해서 , Y의 주변분포 g( y ) 를 만들자.

정규분포는 모든 실수에 대하여 값이 있기 때문에,
Y = Z^2 인것을 생각하면, Y와 Z는 서로 1 : 1 대응이 아니다.
이 경우 Z = + √ y 인 경우 , Z = - √ y 인 경우 나누어서
각각의 야코비안도 구해주고 , z를 결정하는 식 w( y ) , 을 구해서
각각의 g ( y ) 를 구해주면 된다.

마지막 식은 카이제곱분포와 비슷하다.

즉 자유도가 1인 카이제곱 분포이다.
'수리통계학1' 카테고리의 다른 글
| 35강 확률변수 합과 차의 분포 , 누적분포함수법 (0) | 2024.09.04 |
|---|---|
| 34강 변수변환 예제문제, 다변량 정규분포 (0) | 2024.09.01 |
| 32강 확률변수의 변수변환 (1) (0) | 2024.08.28 |
| 31강 다변량 정규분포 (0) | 2024.08.27 |
| 30강 이변량 정규분포 (2) (0) | 2024.08.25 |