조건부 평균과 조건부 분산
-- 복습 --
X = x 가 일어날 확률은 f(x) 이라는 일변수 함수 형태의 확률밀도함수를 이용하여
값을 구했다.
그렇지만 두개의 확률변수가 주어질때 확률은 f(x, y) 이라는 이변수 함수 형태의
결합확률밀도함수를 이용하여 값을 구한다고 배웠다.
또한 주변분포함수도 배웠는데,
주변분포함수란, 결합 밀도 함수가 주어졌을 때,
X만의 , 혹은 Y만의 확률을 구하고 싶을 때 쓰고싶은 확률밀도 함수 형태이다.
보통
X만의 주변분포함수를 g(x) 라고 표현하고
Y만의 주변분포함수를 h(x) 라고 표현하는데 정하기 나름이다.
X, Y 의 결합 확률밀도함수가 f(x, y) 이고, 각각의 주변분포함수를 fx(x), fy(y) 라고 하자.
X = x 로 주어질 때, Y에 대한 조건부 확률밀도함수는

연속확률변수일 경우
X = x 로 고정되어 있을때 Y = y를 움직이면서 Y에 대한 조건부확률밀도함수를 적분하면 확률을 구할 수 있다.
반면
Y = y 로 주어질 때, X에 대한 조건부 확률밀도함수는

연속확률변수일 경우
Y = y로 고정되어있을 때, X = x를 움직이면서 X에 대한 조건부 확률밀도함수를 적분하면 확률을 얻을 수 있다.
조건부 평균에 대해서 알아보자
조건부평균
평균의 개념을 다시 떠올려보자
만일 X에 대한 평균을 구한다면,
X의 평균(기댓값)은 (X의 값) * ( X가 그 값일 확률)의 합이다.
그렇다면,
X = x 일때, Y의 조건부 평균( = 조건부 기댓값) 은
Y 의 값 * Y= y일때, X = x으로 고정될때의 조건부 확률 의 합이다.
조금 복잡한데 ,
X = x 일때, Y의 조건부 평균은 X = x로 고정되어있음을 염두해 두자
그리고 X =x 일때 조건부확률은 Y를 움직여가면서 조건부확률밀도함수를 적분해야 확률값이 나온다.
따라서, X = x인 상황에서 , Y = y1일때 조건부확률+ Y = y2일때 조건부확률 +
Y = y2일때 조건부확률 + ... 더해줘야한다.
이게 두 변수가 있을때 조건부확률의 개념이고
X = x 일때, Y의 조건부 평균은
평균의 정의는 확률변수 * 확률변수가 특정값을 가질때의 확률 을 모든 그 확률변수에 대한 합이므로
Y = y 일때의 y값 * X = x 일때, Y의 조건부확률 을
모든 y에 대하여 적분한 값이다.

무엇이 움직이는가에 따라서 확률이 달라지는지 생각하면 X, Y가 헷갈리지 않는다.
반대로
Y = y 일때 X의 조건부 평균(조건부 기댓값) 에 대해서 생각해보자
평균의 정의를 다시한번 복습하면
평균의 정의는 확률변수 * 확률변수가 특정값을 가질때의 확률 을 모든 그 확률변수에 대한 합 이므로
X = x 일때의 x값 * Y = y 일때 X의 조건부 확률 을 모든 X에 대해서 합을 한것이
Y = y 일때 X의 조건부 평균 이다.
Y = y 일때 X의 조건부 확률은 Y = y로 고정되어있고 X가 움직이면서 조건부 확률밀도함수를 적분한 값이므로
X가 움직인다는 점을 통해 , 조건부 평균 식을 이해할 수 있을 것이다.

지금까지 확률변수 하나만을 가지고 조건부 평균을 생각했다.
Q) 두개?
A) (x)
X = x 인 Y의 조건부 평균이라고 하면 , X 는 x로 고정된거라 상수취급이고
실제로 Y가 움직인거라 , 다룬 확률변수는 Y , 하나뿐이었다.
이번에는 확률변수 하나가 아니라 , 확률변수 식 의 조건부 기댓값은 무엇인지 생각해보자

하지만 이 역시 , X 를 x로 고정해서 ,
u(x, y) 라는 식의 x는 상수처럼 고정한채로 생각해 줘야한다.
위의 식에 친숙하게 접근하기 위해서 ,
예전에 종속확률변수의 평균에대해 학습한 적이있었다.
구하기 위해선, 종속확률변수 * 종속을 취해준 원래 확률변수 가 취할 확률 을 곱해주면 되었다.
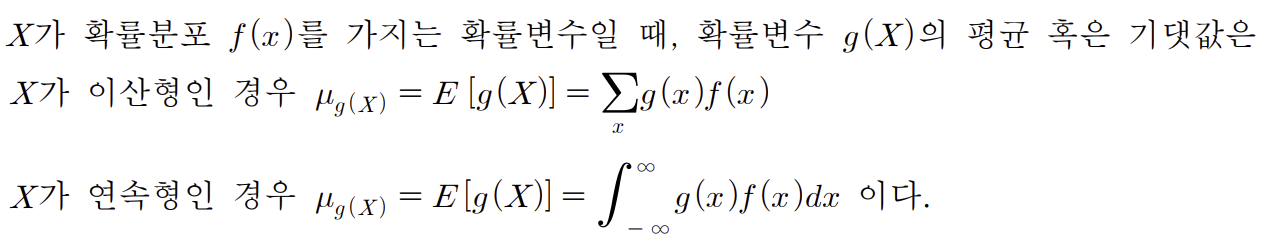
이와 비슷하게
X =x 일때, u(x, y)의 조건부 평균은
u(x, y)라는 일종의 종속확률변수? * 종속을 취해준 원래 확률변수가 취할 조건부확률 을
모든 Y에 대하여 더한 합 이다.
X = x일때 Y의 조건부 분산은 조금 까다롭다.
조건부 분산을 구해보자
분산의 정의는 편차의 제곱의 평균이므로 ,
X = x 일때 Y의 조건부 분산을 구하자고 하면,

한마디로 , 조건부 평균이나 분산을 구하기 위해서
확률이 들어갈 자리에 조건부 확률이 들어가면 되고
평균이 들어갈 자리에 조건부 평균이 들어가면 된다.
조건부 기댓값의 성질
이제까지 조건부평균과 조건부분산의 식은 어떻게 작성하는지 배웠다.
이번에는 조건부 기댓값의 성질은 어떠한지 배워보자

조건부 기댓값의 성질을 차례대로 유도할 것인데
((1)번과 (4)을 제외하고 )
(2), (3), (5) 의 식이 무슨 뜻인지 이해를 하고 유도를 해야 유도가 이해가 된다.
(1) 14강에 선형결합된 서로 다른 확률변수의 평균은 따로 분리될수 있다고 배웠다.
해당식은 평균이 아닌 그저 Z = z 로 고정된 상황에서의 평균이므로 , 따로 분리될 수 있고
(1)과 같은 식을 작성할 수 있다.

(2)

해당 식이 정의가 무엇인지 정확히 이해해야한다.
X = x 로 고정된 상태에서 Y를 움직여가면서 Y의 평균을 구하고 ( = E ( Y l X ) )
이것을 X를 변화시켜갈때 여러개의 E ( Y l X )들이 나올것인데,
이 E ( Y l X ) 들의 평균 을 뜻한다.
그림으로 이해해보자

정의를 식으로 써보면서 증명해보자

노란색을 자세히 보면 Y를 움직여가면서( =dy)
조건부 확률을 y라는 확률변수를 곱해주므로
안의 식은 E ( Y l x) 즉 Y의 조건부 평균 식을 의미한다.
E( E ( Y l x) ) 는 X를 움직여가면서 마치 새로운 확률변수 E ( Y l x) 의 평균을 구하는 것을 의미한다.
따라서 식을 설명해보면,

검은색 E( Y l x ) 를 확률변수라고 생각하면 편하다.
x를 움직여가면서 이 확률변수에다가 확률을 곱하여야 , 평균을 구할 수 있는데
어떤 확률을 곱하여야 정의를 만족할까 생각한다면,
x를 움직이므로 , x만의 확률분포인 x의 주변분포를 확률로 곱해줘야한다.
해당 식을 정리하면,

마지막 식을 정리하면,
(정리하는 방법은 결합분포가 주어졌을때 평균을 구하는 법에서 앞서 다루었다 ( 9강 ) )

따라서 E( E ( Y l x) ) 는 Y의 평균이다.
(3)

이 식도 유도하기 전에 정의를 정확하게 파악해보자
E ( E( u( X, Y) l x) ) 란,
X = x 로 고정된 상황에서 u( X, Y)의 평균( = E( u( X, Y) l x) ) 을
(X를 변화시켜가면 여러개의 E( u( X, Y) l x) 들이 나올텐데 )
평균 내는 것을 의미한다 .

(3)을 유도

(4)

위의 식은
X = x로 고정되어 있기 때문에,
E ( ) 안에 있는 g( X) 의 X 자리에 x를 대입한 상황에서 시작한다는 점을 기억해야함
따라서 g(X)는 상수처럼 고정되어 있으므로 , 밖으로 나올 수 있다.

(5)

이 식은 조금 복잡하다
Y의 분산을
두개의 단항식으로 표현한 식인데,
단항식을 하나하나 분리해서 의미를 파악해보자
E ( Var( Y l X ) ) :
Var( Y l x ) 은 X = x로 고정할 때, Y 의 분산(흩어져있는정도) 를 뜻한다.
즉 Y의 조건부 분산이다.
한단계 더나아가
E( Var( Y l X )) 는 그런 Y의 조건부 분산을 X를 움직여가면서 여러개 만들 수 있다.
여러개 만들어진 분산 ( = 여러개의 Var( Y l X ) ) 들의 평균을 뜻한다.
Var( E ( Y l X ) ) :
X를 x로 고정할 때 Y의 평균을
X를 움직여가면서 얼마나 퍼져있는가를 뜻한다.
이제 E( Var( Y l X )) 의 식을 변형하면서
(5) 식을 유도해보자
평균의 여러가지 정리를 활용한다.
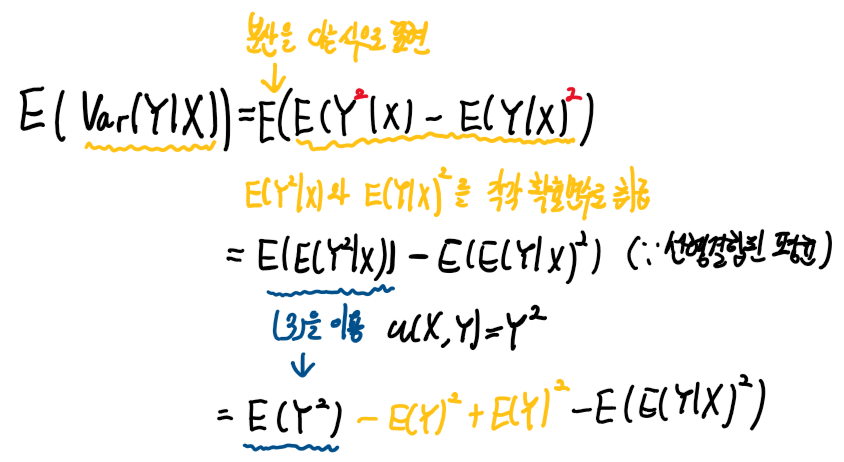
마지막 식은 분산의 정의에 의해

따라서
Var( Y) = E( Var( Y l X )) + Var( E ( Y l X ) ) 식이 성립한다.
5개의 조건부 기댓값의 성질에 대해 살펴봤다.
이번에는
특수한 경우 , 조건부 평균이 어떻게 쓰이는지에 대해서 알아보자
X = x 일 때, Y의 조건부 평균이 x에 대해 선형인 경우
( ⇔ E ( Y l X ) = a + bx )
이산형인 경우를 가정하고 식을 도출할 거지만,
연속형인 경우에도 식이 성립한다.
우선 E ( Y l X ) = a + bx 이 식을 변형한다.

그러면 마지막 식이 나오는데 양변에 fx(x)를 곱해준다.

앞으로 이 식을 기본형으로 쓴다. ( 한번 더 쓸 일이 있음)

먼저
이 식의 양변에 모든 x에 대하여 합을 취한다.
우변은 결합분포가 주어졌을때, y의 평균을 구하는 법을 이용하면 된다. (9강)
그러면 우변은 y의 평균이 나오고
좌변은 모든 경우에 대하여 a + bx라는 확률변수 * 이 확률변수가 나올 확률의 곱의 합을 의미하므로
E( a + bx) 를 의미한다. ( 종속확률변수의 평균 복습!)

위의 기본형으로 남겨두었던 식의 양변에

x를 곱해준 뒤
모든 x에 대하여 합을 취해주자


이제 위의 마지막 식을 공분산을 이용해서 다시 변형을 할 건데
공분산의 정의도 중요하지만
공분산을 다른 식으로 표현 할 수 있다는 것도 기억해 두자


(1) 과 (2)의 식을 연립하여
a와 b를 구한다.

E ( Y l X ) = a + bx 이므로 a와 b에 식을 대입하면,
X = x 일 때, Y의 조건부 평균이 x에 대해 선형인 경우 아래와 같은 식을 만족한다.

조건부 기댓값과 조건부 분산,
조건부 기댓값의 성질
조건부 기댓값이 선형일 경우 조건부 기댓값은 어떻게 생겼는지 에 대해 배웠는데
이를 배운 이유는 이변량 정규분포를 구하기 위함이었다.
이변량 정규분포
X 한개가 정규분포를 따를 때, 정규분포가 어떻게 생겼는지 에 대하여 배웠다면,

X 와 Y
이렇게 변량이 두개가 존재하고
각각이 정규분포를 따를 때,
즉 이변량 정규분포는 어떻게 생기는지 증명을 한다.
근데 증명하기 전에 3가지를 가정한다.
(a) X = x 가 주어졌을 때의 Y는 정규분포를 따른다고 하자.
(b) 이때 Y의 평균 E( Y l x)는 x의 선형함수라고 하자
( 앞서 배운부분이다. 따라서 E( Y l x) 식을 구하지 않고도 알 수 있다. )
(c) 각 x값에 따른 Y의 분산은 모두 같은 상수라고 하자.
이 3가지 가정은 유도할 때 활용된다.
'수리통계학1' 카테고리의 다른 글
| 31강 다변량 정규분포 (0) | 2024.08.27 |
|---|---|
| 30강 이변량 정규분포 (2) (0) | 2024.08.25 |
| 28장 베타분포 (0) | 2024.08.22 |
| 27강 카이제곱 분포, 로그정규분포, 와이블분포 (0) | 2024.08.21 |
| 25강 감마분포와 지수분포의 적용 (0) | 2024.08.20 |