이제 감마분포와 지수분포에 대하여 알아보자
지수분포는 감마분포의 특수한 경우라고 생각하면 된다.
감마분포와 지수분포는
대기이론, 신뢰성 공학 등 여러분야에서 응용되었다.
감마분포는 감마함수에서 이름이 연유되었는데
나중에 감마분포 식을 살펴보면, 그 안에 감마함수가 들어있다.
그래서 먼저 감마함수를 알아야 한다.
감마함수

이때
감마함수에서 알아야할 특징이 있다.
바로 감마함수는 점화식을 발동할 수 있다.

감마함수의 정리를 유도해보자
감마함수를 부분적분함으로써 유도하면 된다.


결론부터 말하자면 위의 값은 0이다.

조금 더 자세한 설명을 적어 두었다.

극한값을 처리할때, 분모에 있는 지수형태의 값이
분자에 있는 일차단항식 보다 더 빠르게 증가한다는 점을 알자
그렇다면 , 분자보다 분모가 더 빠르게 증가하므로, 전체적인 분수 값은 0으로 수렴한다.
이제 뒷부분을 살펴보자

해당 식은 자세히 보면, 감마함수와 비슷하게 생겼다
정확히 말하면 감마함수에 알파대신 알파 - 1을 대입한 식과 비슷하게 생겼다.
그러므로

따라서 알파가 1 이상일때 해당 식이 성립한다.


감마함수의 두번째 특징을 유도해보자
감마함수는 팩토리알을 실수로 확장시킨다는 점에서 의의가 있다.
(b)의 특징은 (a)의 약간 따름정리라고 생각해보자
(a)는 감마함수가 점화식으로서의 특징을 가지고 있다는 것을 말하는데
(a)를 활용해서 (b)를 유도할 수 있다.

감마함수에 1을 대입하면 1이 나오므로
사실상 유도는 끝났다.
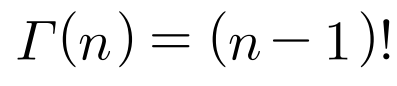
(참고) 감마함수의 특징

감마함수에 1/2 를 넣으면 값으로 루트 파이가 나온다.
이를 설명하기 위해선 바로 전에 배웠던 극좌표계의 이중적분을 활용해야 한다.
정확히 말하면, 직교좌표계에서 극좌표계로 변환시키고 , 그다음 이중적분을 함으로써
감마함수에 1/2 를 넣으면 값으로 루트 파이가 나온다는 것을 계산해 볼 수 있다.
유도해보자

치환적분을 사용해서 식을 어떻게든 정리했지만 ,

지수에 제곱이 되어 있는 형태는 쉽게 적분을 하기 어렵다
그럴때는 전체 식을 한번 제곱해보자
( 이중적분으로 만들기 위함, 이중적분으로 만들어서 , 극좌표계 변환까지 유도해볼 목적으로)
여기서 정적분의 특징을 살짝 언급해주면
정적분은 '값' 이 중요해서
어떤 변수든 상관없이 적분만 잘해주면 된다.
(물론 정적분할 범위에 문자가 들어있으면 신경써야 하지만)

이중적분으로 유도하기 위해서 제곱된 정적분을 x에 대해서 식을정리해보고 y에 대해서 식을 정리해볼것이다.
무슨말인가하면 , 다음과 같다.

그리고 y에 대하여 정리된 정적분을 x에 대하여 정리된 정적분 안에 집어 넣을 수 있다.
( 이중적분에 이런 기술에 대해서 잘 살펴보자, 이렇게 할 수 있는 이유는 x에 대한 정적분식은 x외의 나머지 문자나 수는 상수 취급 하기 때문이다. )

다시 정리해주면

설명에도 나와있듯이 이변수 함수에 대한 이중적분식으로 나타낼 수 있다.
이 이중적분은 엄밀하게 말하면 직교좌표계에서의 이중적분 식이다. (x, y)로 표현되었으니깐
이를 극좌표계의 이중적분 식으로 바꿔보자
왜 그렇냐면 위의 식에서 e의 지수가 원의 방정식 처럼 되어 있다.
이럴때는 이중적분 할때 극좌표계의 이중적분으로 적분하면 조금 더 쉽게 적분할 수도 있다는 점을
알아두자

일단 이중적분은 범위를 잘 살펴봐야한다.
위의 식의 x와 y의 범위를 알아야 r과 세타의 범위를 알 수 있다.
x의 범위는 0 부터 무한대
y의 범위는 0 부터 무한대라는 점을 통해서
(x , y)의 범위는 1사분면 전체라는 점을 알 수 있다.
따라서 r과 세타의 범위는 다음과 같다.

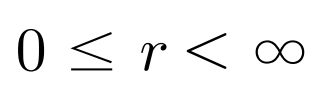
이제 범위를 알았으니
전에 배웠던 , 직교좌표계에서 극좌표계의 이중적분 변환 식을 적용하면 ,


제곱을 했으니깐, 제곱을 풀면 , 유도 끝!

이렇게 감마함수에 대해서 알아봤으니,
감마분포에 대해서 본격적으로 알아보자

감마분포를 잘보면 , 감마함수가 들어있는 걸 알 수 있다.

왼쪽그림은, 베타를 달리했을때 감마분포의 변화를 나타내는 건데
베타가 달라질때, 모양은 달라지진 않는데 크기가 변화하는 모습을 볼 수 있다
반면 오른쪽 그림은 알파를 달리했을때 감마분포의 변화를 나타내는데
알파가 달라질때, 모양이 달라지는 모습을 살펴볼 수 있다.
지수함수에 대해서 알아보자
지수함수는 앞서 말했지만 감마함수의 특수한 경우임을 알아두자

감마분포와 지수분포를 소개했으니 이제 각 분포의 특징들을 유도해보자
먼저 감마분포가 확률분포의 조건을 만족하는지를 알아보자
확률분포의 조건을 만족한다는 것은
반복적으로 설명했지만 모든 경우의 확률의 합이 1 이라는 뜻이므로
맞춰서 유도를 하면 된다.

이 식의 양변에 감마함수를 나눠주자
좌변이 1이 되게끔 한다.

이 식을 감마분포로 변환하기 위해서
문자를 치환한다.

위의 식의 t 대신 x를 집어넣는다면,

이 식을 감마분포와 최대한 유사하게 만들어보자

이렇게 감마분포가 확률분포의 조건을 만족함을 알게되었다.
감마분포의 평균과 분산에 대한 정리를 알아보자

유도)
우선 평균의 정의를 이용해 식을 작성한다.

문자를 치환한다.

식을 정리한다.

감마함수의 평균 유도 끝!
감마함수의 분산을 유도해보자


감마분포 분산 유도가 끝이 났다.
감마분포 평균과 분산 의 따름 정리가
지수분포의 평균과 분산이다.

'수리통계학1' 카테고리의 다른 글
| 27강 카이제곱 분포, 로그정규분포, 와이블분포 (0) | 2024.08.21 |
|---|---|
| 25강 감마분포와 지수분포의 적용 (0) | 2024.08.20 |
| 극좌표계에서의 이중적분 (0) | 2024.08.19 |
| 21강 연속형 균일분포, 정규분포, 표준정규분포 (0) | 2024.08.17 |
| 20. 포아송 분포와 포아송 과정(1) (0) | 2024.08.16 |