극좌표계에서의 이중적분

 

 

극좌표계에서 이중적분을 어떻게 하는지 배워보자 

 

이걸 알아야 24강에 배울 감마분포를 이해할 때 도움이 된다. 

 

예전부터 배운 x축 y축 으로 이루어진 사분면에 한 점을 (x , y) 두어서 

위치를 나타낸다고 생각할 때 

 

이것을 직교좌표계를 이용했다고 말한다. 

 

출처: 네이버 지식백과

 

이것이 직교좌표계이다. 흔히 x, y를 통해서 위치를 표시한다. 

 

직교좌표계와 다른 좌표계인 

 

극좌표계에 대해서 알아야한다.

 

극좌표계는 거리와 각을 통해 위치를 표시하는 좌표계이다.

 

 

 

각각의 점은 서로 다른 r 과   θ(세타) 을 가지고 있기 때문에

극좌표계에서는 (x, y) 대신 ( r , θ )를 이용해서 위치를 표현할 수있다.

 

​각은 1사분면만 제한되어 있지 않기 때문에 1~ 4사분면의 점의 위치는 충분히 r 과 θ (세타)를 이용해서 표현할 수 있다. 

 

극좌표계에 조금 더 익숙해져보자 

빨간색에 위치한 점들은 모두 같은 r2를 공유하고 있다. 

(r은 원점과 점과의 거리 , 부채꼴로 생각해본다면, 반지름이다.) 

 

파란색에 위치한 점들은 모두 같은 r1을 공유하고 있다. 

 

 

 

 

주황색에 위치한 점들은 모두 θ1을 공유하고 있다. 

 

초록색에 위치한 점들은 모두 θ2를 공유하고 있다. 

 

즉 모양을 보면, 극좌표계는 원, 부채꼴과 연관되어 있다. 

 

 

아무튼 극좌표계는 (x, y) 가 아닌 ( r, θ)를 이용해서 점을 표시하는 좌표계를 뜻한다. 

 

극좌표계

 

 

 

R의 영역에서 이중적분을 구하고 싶을때 

 

극좌표계를 모른다고 생각하면 

 

직교좌표계를 이용해서, x와 y에 대하여 f(x, y)를 x에 대하여 한번 적분하고 

y에 대하여 한번 적분하는 이중적분을 하면 되지만, 그렇게 했을때 

 

복잡한 경우가 있다. 

 

그런 경우, 

 

극좌표계를 이용하면 쉽게 풀리는 경우가 존재한다. 

 

주로 넓이가 원(ex. x2 + y2) 으로 되어 있거나, 부채꼴 모양으로 되어있으면 극좌표계를 한번 생각해보자 

 

의외로 쉽게 풀릴 수 있다. 

 

위의 그림에서 R의 영역에서 이중적분을 구하기 위하여 

 

극좌표계에서의 이중적분을 이용한다고 하면, 

 

식은 다음과 같다. 

 

R이라는 영역의 극좌표계에서의 이중적분 식은 다음과 같다. 나중에 감마분포의 특성에 대해서 유도할때 쓰인다.

 

 

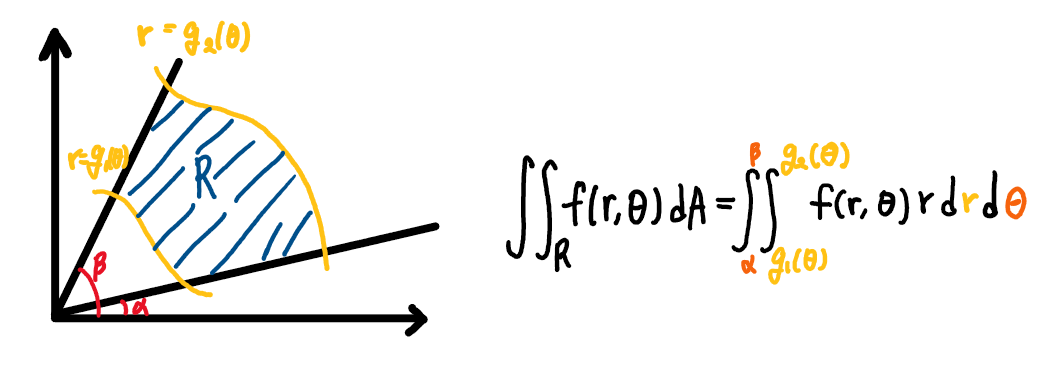
근데 여기서 중요한 점이 있다. 

 

극좌표계에서 이중적분을 할 때 r을 빼먹으면 안된다는 점이다. 

 

빨간색으로 표시한 r, 이는 R이라는 영역을 이중적분할때, 즉 R이라는 영역의 부분인 잘게 쪼개진 극사각형의 식과 연관이 있다.

 

흔히 직교좌표계에서 이중적분 식은 다음과 같은데 

 

 

위는 직교좌표계에서의 주어진 영역을 이중적분한 식, 안의 적분은 x에 대하여 적분, 바깥의 적분은 y에 대하여 적분한다는 것을 표기로 알 수 있다. 아래는 극좌표계에서 주어진 영역을 이중적분한 식

 

극좌표계에서는 이중적분을 할때 r이 추가되어야 한다. 

 

이유를 살펴보자 

 

우선 정적분이라는 것은 영역의 넓이는  잘게 쪼갠 부분들을 다 더한다 라는 개념을 알고, 

 

이를 극좌표계에 적용하면 된다. 

 

잘게 쪼갠 부분을 △A라고 하자 , 

R은 잘게 쪼갠 부분인 △A의 합으로 구성되어 있고 

△A은 다시 더 잘게 쪼개서 n -> ∞ 일때의 정말 잘게 쪼개진 부분을 dA라고 하자 

 

그리고 dA의 의미를 

 

직교좌표계와 

 

극좌표계 에서 비교해보자 

 

 

직교좌표계의 경우 dA의 의미는 

 

R의 일부분인 A의 넓이를 n -> ∞ 처럼 한없이 쪼갰을때의 A의 값을 의미한다. 

 

 

식으로 표현하면 

 

 

dxdy 는 직교좌표계의 이중적분에서 그대로 반영된다. 

 

반면

 

극좌표계에서의 이중적분에서 

 

dA를 살펴보면, 

 

부채꼴로 생각해본다면, R의 영역은 작은 극사각형의 합으로 이루어져 있다.

 

 

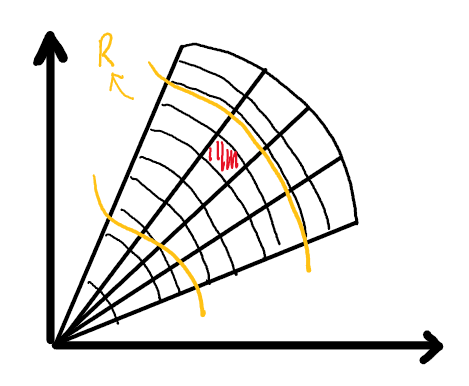
R의 일부분인 해당 그림의 빨간색 영역 △A를 

 

n->∞ 처럼 한없이 쪼갰을때의 값을 의미한다. 

 

해당 영역을 극사각형 이라고 하는데 

 

직관적으로 말하면, 

 

r이 아주 조금 늘고, θ 세타가 아주 조금 늘었을때, 

아주 조금 늘어난 사각형의 영역을 극사각형이라고 한다. 

 

극사각형을 조금더 확대해서 살펴보면 다음과 같다. 

 

즉 극사각형은 

 

큰 부채꼴 (반지름이 rk+1) - 작은 부채꼴 ( 반지름이 rk) 로 구할 수 있다. 

 

부채꼴의 넓이는 1/2 * 반지름의 제곱 * 둘러싼 각  θ(세타) 로 구할 수 있고 , 

 

R은 이러한 극사각형으로 이루어져 있으므로 

 

R의 부분을 나타내는 △A은 극사각형이다. 

 

△A을 식으로 나타내면 다음과 같다. 

 

θ 가 아주 조금 증가했을때, 영역도 △Ak만큼 아주 조금 증가한다. △Ak 를 식으로 나타내면 위와 같다.

 

 

 

이제 n -> ∞ 처럼 아주 잘게 쪼개보자 그렇다면 △Ak의 증분 값은 아주 미세할 만큼 작을것이다. 

이를 dA라고 표현하고 , 

 

여기서 직관적으로 생각해보면 

 

무한대로 갈만큼 아주 미세하게 쪼개기 때문에, 

결과적으로 극사각형의 모습은 아주 미세한 하나의 점으로 보일것이다. 

 

 

그렇게 된다면 결국 rk+1 과 rk는 같아질것이고 , 

한때는 극사각형이었던 미세한 점에서와 원점사이의 거리인 r 로 같아질 것이다. 

 

이를 고려하여 위에서 적은 △Ak를 n -> ∞ 극한으로 보낸다면, 

다음과 같다. 

 

따라서 극좌표계에서 이중적분할시 

 

극사각형을 n -> 무한대로 보낼때 

 

r이 남겨져있기 때문에 

 

r를 빼먹으면 안된다. 

 

빨간색으로 표시한 r, 이는 R이라는 영역을 이중적분할때, 즉 R이라는 영역의 부분인 잘게 쪼개진 극사각형의 식과 연관이 있다.

 

 

해당 식을 잘 알고 있자. 

 

 

 

여기서 추가적으로 알아야 할 부분이 있다 

 

 

직교좌표를 극좌표로 바꾸는 방법이다. 

 

 

(x , y)를 (r*cos θ, r*sin θ) 로 표현할 수 있으므로 

 

직교좌표를 극좌표로 변환할 땐, f(x , y)이 주어져 있다면, 

 f(x , y) 를 f( r*cos θ, r*sin θ) 로 표현하고 , 

dr에 대해서 , dθ 에 대하여 이중적분을 하면 된다. 

 

직교좌표를 극좌표로 변환할시, 이중적분