대표적인 이산확률분포 중 마지막
포아송 분포에 대해 알아보자
포아송 분포
포아송분포는 포아송실험에서 발생하는 결과들의 분포들 말하는데
포아송실험이란 주어진 시간간격 또는 일정한 영역 내에서
관찰하고자 하는 결과가 몇번이나 발생하는가를 산출하는 실험이다.
즉 일정한 영역 내에서 발생하는 결과들의 수를 확률변수 X로 두고
이 X 값을 산출하는 실험이다.
예를들어서..
일정 시간 동안에 방문한 고객의 수
사무실에 걸려오는 시간당 전화수
단위 면적 당 인구 수
특정 면적의 숲의 소나무의 수 등
실생활에서 포아송 실험을 볼 수 있다.
포아송실험을 할 때 주의해야할 점이 있다.
포아송 과정
1. 단위 시간 간격이나 일정 영역에서 발생하는 결과의 수는
서로 다른 시간 간격이나 영역에서 발생하는 수와 독립이다
= 건망성 ( no mermory 라고함) 특징
2. 매우 짧은 시간 간격이나 작은 영역에서 단 한번의 결과가 일어날 확률은
시간 간격이나 영역의 크기에 비례하고,
시간 간격이나 영역의 크기의 외부에서 발생하는 결과의 수와는 무관하다
3. 매우 짧은 시간 간격이나 작은 영역에서 둘 이상의 결과가 일어날 확률은
무시할 수 있다.
포아송 확률변수는 포아송 실험에서 결과의 발생횟수 X를 뜻한다.
포아송 분포는 다음과 같다.

포아송 분포라는 건 제한된 영역안에 특정한 몇번이 발생할 확률을 뜻하는건데
평균적으로 몇번이 나타날지 람다 * t 가 주어진다.
t = 1 이면, 평균적으로 람다 번 발생한다고 주어짐
포아송 분포의 확률분포 성질 유도

성질 유도할 때 매클로빈급수(테일러 급수) 를 알아야한다.
다음은 매클로빈 급수중 하나이다.

몇번 이하 발생할 확률을 나타내는 누적포아송 분포표가 있으니 참고해보자
예제를 풀어보자

해당예제에서 1/1000초 동안 카운터를 통과하는 방사능 입자의 평균수가 4이므로
람다*t = 4 이다. (평균이 4 로 주어졌으니깐)
1/1000초 동안이라는 시간간격에서 평균이 4 로 주어졌고 묻는건
평균이 4라는 정보가 주어진 상태에서 6개가 일어날 확률을 묻는것이므로
포아송분포를 사용한다.
포아송 분포 식에 값을 대입하면 식이 이렇게 나오는데

복잡하다. 이럴때 식을 조금 간편하게 쓸수 있는게 누적 포아송 분포표이다.
누적포아송 분포표를 활용한다고 생각한다면
6개가 일어날확률은 6개 이하가 일어날 확률 - 5개 이하가 일어날 확률 로 구할수 있으므로

답은 0.1042가 나온다.
포아송분포의 평균과 분산에 대해서 알아보자

포아송 분포의 평균을 유도해보자
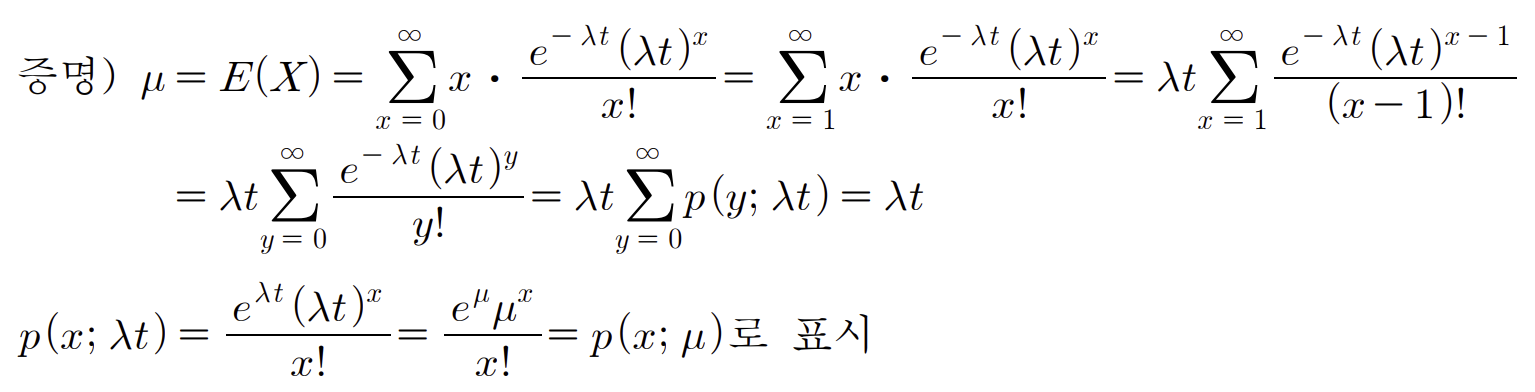
포아송분포의 분산을 유도해보자
이를 위해선 E(X(X-1))의 식을 포아송분포의 형태와 가깝게 표현해야한다.


분산 역시 비슷한 방법으로 유도하면
분산의 값이 평균이 나온다.
'수리통계학1' 카테고리의 다른 글
| 극좌표계에서의 이중적분 (0) | 2024.08.19 |
|---|---|
| 21강 연속형 균일분포, 정규분포, 표준정규분포 (0) | 2024.08.17 |
| 17강 이항분포와 다항분포 (0) | 2024.07.04 |
| 16강 이산형 균일분포 (0) | 2024.07.04 |
| 15강 체비셰프 정리 (0) | 2024.07.03 |