이어서
이항분포의 평균과 분산에 대해서 알아보자
· 이항분포의 평균과 분산

증명은 베르누이분포의 평균과 분산(16강) 그리고 선형결합된 확률변수의 평균,분산(14강) 을 이용한다.
성공횟수를 나타내는 이항분포의 확률변수를 정의하자


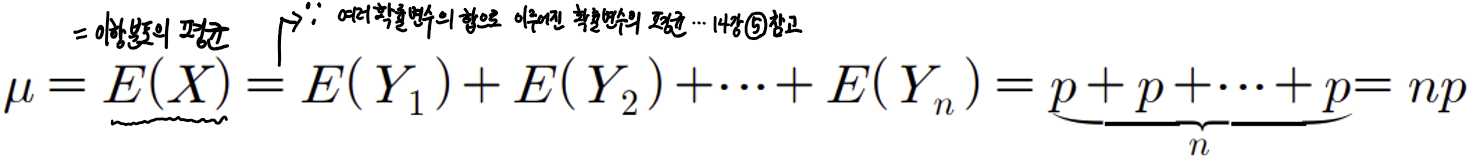


다항분포에 대해서 알아보자
· 다항분포
이항분포란 두가지 결과가 나오는 하나의 시행을 여러번 반복했을 때의 확률분포를 뜻한다.
다항분포는 두가지 결과가 아닌 여러 개의 결과가 나오는 하나의 시행을 여러번 반복했을 때의 확률분포를 뜻한다.
둘다 하나의 시행에서의 여러개(이항분포일 경우 두개)의 결과는 서로서로 독립적이다.
즉 둘다 여러번의 시행을 한다고 말했는데,
구체적으로 말하면 둘다 n번의 시행을 한다.
그리고 둘다 각각의 시행이 서로 독립적이다.
이항분포의 경우, n번의 시행들은 서로서로 독립적이다.
첫번째 시행에서 결과(ex. 성공 or 실패)가 일어났다고 해서
두번째 혹은 k번째(k= 1 or 2 or ... or n) 시행에서의 결과가 첫번째 시행의 결과에 의해 영향을 받는 일은 없다.
다항분포도 마찬가지로, n번의 시행들이 서로 독립적이다.
첫번째 시행에서의 결과(E1 , E2, E3...) 가 일어났다고 해서
두번째 혹은 k번째(k= 1 or 2 or ... or n) 시행에서의 결과가 첫번째 시행의 결과에 의해 영향을 받는 일은 없다.
다항분포의 식을 끌어내기 위하여,
1.다항실험의 이해
2.다항분포의 확률변수 이해
3. 다항분포의 확률을 구하는 법 이해
이 세가지 이해가 필요하다.
다항분포를 조금 더 구체적으로 설명하자
1. 다항실험의 이해
다항실험을 했을때 확률분포를 다항분포라고 한다.
다항실험이란 여러개의 결과가 가능한 시행을 여러번 하였을 경우를 뜻한다.
하나의 시행으로 여러개의 결과가 나온다.
식으로 표현하면 이렇다.

해석하면
E1이라는 사상이 일어날 확률을 p1이라고 하고,
E2라는 사상이 일어날 확률을 p2라고 한다.
하나의 시행에서 여러개의 결과가 나온다고 했는데
만약 하나의 시행에서 k개의 결과가 나온다고 하면,
Ek라는 사상이 일어날 확률은 pk이다.
각각의 사상은 서로 독립적이다.
즉 E1이라는 사상이 일어난다고 해서 이것이 E2라는 사상에 영향을 끼치지 않는다.
여기서 하나의 시행에는 k개의 결과만 나오고
그외의 결과는 나오지 않는다.
그리고 각각의 사상은 독립적이므로 ,
사상이 나올 확률을 다 더하면 1이 나온다.

이항분포에서의 확률변수란
한번의 시행에서 두가지 결과( ex. '성공' vs '실패' ) 가 나오는데
n번의 시행에서 한쪽의 결과( 보통은 '성공' )가 나올 횟수 를 X라고 한다.
그렇다면
다항분포에서의 확률변수는 무엇일까?
2.다항분포의 확률변수 이해
한번의 시행에서 여러가지 결과( E1, E2, E3, E4, .... Ek(가능한 결과가 k개라고 한다면) ) 가 나오는데
조금 복잡하게
n번의 시행에서 E1이 x1번 발생, E2 가 x2번 발생 , .... , Ek가 xk번 발생한 횟수를 다항분포에서의 확률변수라고 하고
표현은 이게 하나의 횟수만 체크하는게 아니라 여러개의 횟수를 체크해야해서
표기를 조금 다르게 해야한다.
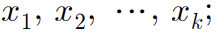
(기호에 대해서 설명한다면, 확실한건 n번의 시행을 한다고 했으므로 ,
E1이 일어날 횟수(=x1) 나 E2가 일어날 횟수(=x2) 나 Ek가 일어날 횟수(=Ek)가 어떤지 간에
x1 + x2 + ... + xk = n 이라는 식이 성립한다. )

예를 들어서 하나의 시행에서 3개의 결과가 나온다고 할 때, 이 시행을 n번 반복한다면,
3개의 결과를 각각 E1(ex. 스페이스) , E2(ex. 클로버) , E3(ex. 하트) 라고 한다고 했을때,
E1이 일어나는 횟수를 x1
E2가 일어나는 횟수를 x2
E3가 일어나는 횟수를 x3
이라고 둘 수 있다.
만일 E1이 일어날 횟수가 2번 , E2가 일어날 횟수를 1번 , E3가 일어날 횟수를 0번 이라고 한다면
구하고자 하는 확률의 확률변수는 2 , 1, 0 ; 으로 표현할 수 있다.
(예전에 확률변수에 대해서 다룰땐 그땐 X= 2일 확률은? 이런식으로 생각해왔다.
즉 하나의 확률변수에 대한 확률만을 생각해왔다.
그러다가 결합확률분포에 대해서 배우면서 여러개의 확률변수 (주로 X와 Y 라는 두개의 확률변수가있을때 확률)
에 대한 확률을 생각했다.
다항분포도 마찬가지로 여러개의 확률변수(x1, x2, ..., xk) 에 대한 확률
즉 하나의 확률변수가 아닌
여러개의 확률변수(= 다변량 확률변수) 에 대한 확률을 알려주는 확률분포이므로 ,
다항분포는 결합확률분포중 하나이다. )
앞서 언급한 나의 시행에서 3개의 결과에서
E1이 일어날 횟수가 2번 , E2가 일어날 횟수를 1번 , E3가 일어날 횟수를 0번 일 확률을 구하려고 하면
확률변수가 2 , 1, 0 ; (= (x1, x2, x3 ;))인 확률을 구하면 된다.
그럼 이 확률은 어떻게 구할까에 대해서 알아보자
3. 다항분포의 확률을 구하는 법 이해
이항분포의 경우 확률을 구하는 법의 연장선이라고 생각하면된다.
이항분포의 확률을 구할 때 (경우의 수 ) * 확률 이란 아이디어를 이용해서
구하라고 언급한 적이 있다. (16강_참고)
다항분포의 확률도 마찬가지로
(경우의 수) * 확률 을 이용해서 구하면 된다.


이제 다항분포를 식으로 나타내보자

'수리통계학1' 카테고리의 다른 글
| 21강 연속형 균일분포, 정규분포, 표준정규분포 (0) | 2024.08.17 |
|---|---|
| 20. 포아송 분포와 포아송 과정(1) (0) | 2024.08.16 |
| 16강 이산형 균일분포 (0) | 2024.07.04 |
| 15강 체비셰프 정리 (0) | 2024.07.03 |
| 14강. 선형결합된 확률변수의 평균과 분산 (0) | 2024.07.02 |